9月1日更新的2021年江苏公务员考试每日一练是数量关系题，多做公务员考试模拟题练习不仅有利于掌握考点，而且能够帮助保持题感，潜移默化中熟悉命题规律，提高公务员考试做题准确率。

　　1、瓶里装满浓度为50%的溶液，倒出10L后装满水，再倒出5L后装满水，瓶里溶液的浓度不超过36%，则该瓶的容积最大是多少？（ ）

　　A、20L

　　B、30L

　　C、40L

　　D、50L

　　2、从1、2、3、4、5、6、7、8、9九个数字中任选两个数字，要使这两个数字的和为偶数，一共有多少种组合？（ ）

　　A、12种

　　B、14种

　　C、15种

　　D、16种

　　3、将一个用若干个边长为1厘米的小正方体拼成的长为20厘米、宽为10厘米、高为8厘米的长方体的表面染上颜色，那么只有一面被染色的小正方体与未被染色的小正方体的比为：（）

　　A、25：36

　　B、36：25

　　C、107：108

　　D、108：107

　　4、一批商品，按原价销售了60%以后打五折出售，最后发现总的利润率是20%，问按原价销售的利润率是多少？（ ）

　　A、30%

　　B、40%

　　C、50%

　　D、60%

　　5、某班评定学生奖学金时，规定平时分、期中分和期末分的排名均在班级前30%的学生才有资格获取。现从该班任选一名学生，其有资格获取奖学金的概率最高为（ ）。

　　A、2.7%

　　B、10%

　　C、30%

　　D、65.7%

　　1、D

　　第一步：分析问题

　　本题为浓度问题，为溶液不变型。若溶液不变，则最后溶液的浓度为最初浓度乘以每次倒出溶液后剩下的百分比。由于本题中问的是该瓶容积最大是多少，故可采用代入排除的方法进行解决即可，并从最大的数字开始代起。

　　第二步：计算过程

　　选项中最大的数字为50L，故从D选项开始代入。原溶液浓度为50%，倒出10L，相当于倒出了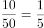，再加满水后，浓度为50%×（1-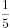）；再倒出5L，相当于倒出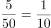，再加满水后，浓度为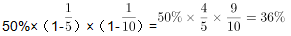，满足“瓶里溶液的浓度不超过36%”，说明D选项符合。由于问的是“容积最大是多少”，D选项即为正确答案。

　　故正确答案为D。

　　2、D

　　第一步：分析问题

　　本题为排列组合问题，一共9个数字，其中有5个奇数、4个偶数。若任选两个数字，和为偶，则挑出来的数字要么同为奇数，要么同为偶数（奇数+奇数=偶数，偶数+偶数=偶数）。由于任意挑出来的两个数与顺序无关，故为排列问题。

　　第二步：计算过程

　　任意挑出来的两个数，和为偶包括两种情况:（1）挑出来的两个数均为奇数，由于共有5个奇数，故从5个奇数中任意挑出2个奇数的挑法有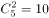：种；（2）挑出来的两个数均为偶数，由于共有4个偶数，故从4个数中任意挑出2个偶数的挑法有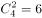：种。

　　这两个数字的和为偶数，共有的组合数为10+6=16种。

　　故正确答案为D。

　　3、A

　　第一步：分析问题

　　本题为几何问题。题目中给了小正方体的边长以及长方体的长、宽、高，故可知长方体的长、宽、高上的小正方体数。一面被染色的小正方体应在表面上并且未在棱上，未被染色的小正方体应该在长方体的内部，即不在外表面。

　　第二步：计算过程

　　由于每个小正方体的长为1厘米，长方体长为20厘米，则长方体长边上的小正方体的个数为20个；同理，长方体宽边上的小正方体的个数为10个；长方体高边上的小正方体的人数为8个。

　　对于长、宽构成的一个面来说，只有一面被染色的小正方体个数为：（20-2）×（10-2）=18×8=144个；同理，对于宽、高构成的一个面来说，只有一面被染色的小正方体个数为：（10-2）×（8-2）=8×6=48个；对于长、高构成的一个面来说，只有一面被染色的小正方体个数为：（20-2）×（8-2）=18×6=108个。由于长、宽构成的面，宽、高构成的面，长、高构成的面各有两个，故在长方体中，只有一面被染色的小正方体个数共有：2×（144+48+108）=600个。

　　未被染色的小正方体有：（20-2）×（10-2）×（8-2）=864。

　　则只有一面被染色的小正方体与未被染色的小正方体的个数之比为600:864=25：36。

　　故正确答案为A。

　　4、C

　　第一步：分析问题

　　本题为经济利润问题。由于题目中给出的数据均是百分数，且涉及到了数量，故可采用赋值法，对成本和数量进行赋值。若要求出按原价销售的利润率，需要求出原价是多少。若要求出原价，则可利用已知信息，利用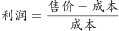：、总售价=打折前售价+打折后售价，进行求解。

　　第二步：计算过程

　　将一件商品的成本赋值为10，商品的总数量赋值为10，设售价为x。销售了60%，相当于售出了6件，则前6件的总售价为6x；剩下的打5折，相当于后4件每件的售价为0.5x，则后4件的总收入为0.5x×4=2x，10件的总售价为6x+2x=8x。总成本为10×10=100元。根据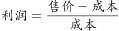可以列出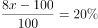，解得x=15元。若按原价售出，则销售的利润率为：。

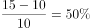　　故正确答案为C。

　　5、C

　　第一步：分析问题

　　问题求获奖的概率最高是多少，要使被选中的学生获奖的概率尽量高，就要使符合获奖条件的人数尽量多，即平时分、期中分和期末分的排名均在班级前30%的学生是完全相同的人。

　　第二步：计算过程

　　根据题意，假设该班有100人，则平时分、期中分和期末分均排名班级前30%的各有30人，获奖人数最多为30人，即平时分、期中分和期末分的排名均在班级前30%的学生相同。此时任选一名学生，其有资格获取奖学金的概率为30/100=30%。

　　故正确答案为C。