1.时钟的分针和时针现在恰好重合，那么经过多少分钟可以成一条直线?

　　A.62.5

　　B.64.5

　　C.32(6/11)

　　D.32(8/11)

　　2.从左向右编号为1至2012号的2012名同学排成一行，从左向右1至12报数，报数为12的同学原地不动，其余同学出列；然后留下的同学再从左向右1至12报数，报数为12的留下，其余同学出列；留下的同学第三次从左向右1至12报数，报到12的同学留下，其余同学出列，那么最后留下的同学中，从左边数第一个人的最初编号是(    )。

　　A.1884

　　B.288

　　C.1653

　　D.1728

　　3.如图，学校操场的400米跑道中套着300米小跑道，大跑道与小跑道有200米路程相重。甲以每秒6米的速度沿大跑道逆时针方向跑，乙以每秒4米的速度沿小跑道顺时针方向跑，两人同时从两跑道的交点A处出发，当他们第二次在跑道上相遇时，甲共跑了多少米?（ ）

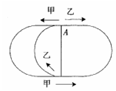
　　A.480

　　B.540

　　C.660

　　D.720

　　4.甲、乙两人分别从A、B两学校同时出发，相向而行。其中甲骑自行车，乙步行，甲的速度是乙的3倍，甲用时20分钟后到达B校后立即返回，两人第二次相遇后，乙再走(    )分钟后才能到达A校。

　　A.30

　　B.45

　　C.50

　　D.55

　　5.一块三角地带，在每个边上植树，三个边分别长156m、186m、234m，树与树之间距离为6m，三个角上必须栽一棵树，共需多少树？（    ）

　　A.93

　　B.95

　　C.96

　　D.99

　　江苏公务员考试网（http://www.jsgwy.com.cn/）解析　题目或解析有误，我要纠错。

　　1.答案: D

　　解析:

　　根据时钟问题的基础知识可知，分针速度6°/min，时针速度0.5°/min，速度差为6-0.5=5.5°/min。当时针和分针成一条直线时，分针比时针多走了半圈，即路程差为180°，所以两次重合间隔时间为180÷5.5=360/11，选择D选项。

　　2.答案: D

　　解析:

　　第一次报数后留下的同学最初编号都是12的倍数；第二次报数后留下的同学最初编号都是144的倍数；第三次报数后留下的同学最初编号都是1728的倍数。所以最后留下的只有一位同学，他的最初编号是1728。

　　3.答案: C

　　解析: 根据题意可知，甲、乙只可能在AB右侧的半跑道上相遇。易知，小跑道上AB左侧的路程为100米，右侧的路程为200米，大跑道上AB的左、右两侧的路程均是200米。当甲第一次到达B点时，乙还没有到达B点，所以第一次相遇一定在B点右侧某处。而当乙跑完一圈到达A点需要300÷4=75秒，甲跑了6×75=450米，在A点左边50米处。所以当甲再次到达B处时，乙还未到B处，那么甲必定能在B点右边某处与乙第二次相遇。从乙再次到达A处开始计算，还需(400-50)÷(6+4)= 35秒，甲、乙第二次相遇，此时甲共跑了75+35=110秒，从开始到甲、乙第二次相遇甲共跑了6×110=660米，应选择C。

　　4.答案: A

　　解析:

　　根据题目条件可知，甲骑车走完A、B两学校全程的时间是乙步行走完全程时间的三分之一，故乙始终处在第一次从B校走向A校的过程中。所以第一次相遇是迎面相遇，第二次相遇是甲从后面追上乙。假设甲、乙的速度分别为3和1，则全程的距离为3×20＝60。从开始出发到第二次相遇时，甲所走路程比乙所走路程多了一个全程，用时60÷(3—1)＝30(分钟)。乙走完全程需要用时60÷l＝60(分钟)，所以还需要再走30分钟才能到达A校。

　　5.答案: C

　　解析:

　　植树问题的关键点：在非闭合路线（如直线）上植树时，若两端都植树，棵数=总路长÷间距+1；在闭合路线上（如圆）上植树时，棵数=总路长÷间距。因此，本题需植树：（156+186+234）÷6=96棵。因此，本题答案为C选项。