1.有一池水，池底有泉水不断涌出，要想把水池的水抽干，10台抽水机需抽8小时，8台抽水机需抽12小时，如果用6台抽水机需抽多少小时？（  ）

　　A.16

　　B.20

　　C.24

　　D.28

　　2.药厂使用电动研磨器将一批晒干的中药磨成药粉，厂长决定从上午10点开始，增加若干台手工研磨器进行辅助作业，他估算如果增加2台，可在晚上8点完成。如果增加8台，可在下午6点完成，问如果任务增加一倍还希望在下午3点完成，需要增加多少台手工研磨器？（   ）

　　A.62

　　B.68

　　C.70

　　D.74

　　E.81

　　.85

　　.88

　　.90

　　3.假设某地森林资源的增长速度是一定的，且不受到自然灾害等原因影响。那么若每年开采110万立方米，则可开采90年，若每年开采90万立方米则可开采210年。为了使这片森林可持续开发，则每年最多开采多少万立方米林木？（  ）

　　A.30

　　B.50

　　C.60

　　D.75

　　4.有一块草地，上面的青草每天都生长得一样快。这块草地上的青草供20头牛吃，可以吃12天，或者供25头牛吃，可以吃8天。某人有牛70头，如果要保证青草不被吃完，需要在几块这样的草地上放牧?(    )

　　A.7

　　B.8

　　C.9

　　D.10

　　5.有一个灌溉用的中转水池，一直开着进水管往里灌水，一段时间后，用2台抽水机排水， 则用40分钟能排完；如果用4台同样的抽水机排水，则用16分钟排完。问如果计划用10分钟将水排完，需要多少台抽水机？（  ）

　　A.5台

　　B.6台

　　C.7台

　　D.8台

　　江苏公务员考试网（http://www.jsgwy.com.cn/）解析　题目或解析有误，我要纠错。

　　1.答案: C

　　解析:

　　假设，泉原有水量为x，单位时间涌出的水量为y，根据题意可得：x＝(10-y)×8，x＝(8-y)×12，解得x＝48，y＝4。假设如果用6台抽水机需要用时为T，则可得48＝（6－4）×T，解得T=24（小时），故正确答案为C。

　　注：牛吃草问题，题目表述为某量以一定的速度均匀增张，同时又以另一速度被均匀消耗，均可直接套用公式：草原原有草量＝（牛数－每天长草量）×天数，在本题公式可变形为 ：泉原有水量＝（抽水机数－每小时时间涌出水量）×小时数。

　　2.答案: D

　　解析: 设原有电动研磨器为N台，需要增X台手工研磨器，根据牛吃草公式有： /Y=(N +2)10；Y=(N +8)8 /解得N=22，Y=240；代入2Y=（N+X）5解得X=74 /故选择D选项

　　3.答案: D

　　解析:

　　假设原有森林资源、每年增长量分别为N万立方米和x万立方米，则根据题意可得：N＝(110－x)×90，N＝(90－x)×210，解得N＝3150，x＝75。为了可持续开发，则每年开采的量等于每年的增量即可，也即为75万立方米。故正确答案为D。

　　4.答案: A

　　解析: 假设这块草地原有草量为x，每天长草量为y，每头牛每天吃草的量为1，则根据公式可得：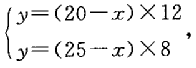

　　解得x＝10，这块草地每天的长草量够10头牛吃。要保证青草不被吃完，需要在70÷10＝7(块)这样的草地上放牧。

　　5.答案: B

　　解析:

　　设未用抽水机时中转水池共有水N，每分钟进水Y，根据题意可得N＝(2－Y)×40，N＝(4－Y)×16，解得Y＝2/3，N＝160/3。因此10分钟将水排完，需要抽水机160/3÷10＋2/3＝6台，故正确答案为B。

　　公式：在牛吃草模型背景下，公式为N＝(牛数－Y)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量；Y表示专门吃新增加草量所需要的牛数。