1、裂项相消

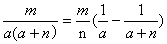
　　2、乘方尾数

　　①指数除以4，留余数（如果余数为0，则看成4）；

　　②底数留最末位。

　　以3为例，从1次方开始尾数分别为3、9、7、1、3、9、7、1、3、9、7、1······，从这里可以看出，3的幂次由低到高尾数分别为3、9、7、1四个数字循环，因此要求3n的尾数，只要看n÷4余数是几就可以确定n次方尾数会是3、9、7还是1了。

　　3、星期日期

　　平年闰年判定：四年一闰，百年不闰，四百年再闰。

　　大小月：大月31天(1、3、5、7、8、10、12)

　　小月30天(4、6、9、11)

　　2月28天(或29天)

　　4、分数比例

　　若a：b=m：n（m、n互质），

　　则a是m的倍数，b是n的倍数；

　　若a＝m/n×b，则a＝m/（m＋n）×（a＋b），即a＋b是m＋n的倍数；

　　5、尾数法

　　选项尾数不同，且运算法则为加、减、乘、乘方运算，优先使用尾数进行判定；

　　6、等差数列

　　和=（首项＋末项）×项数÷2＝平均数×项数＝中位数×项数；

　　项数=（末项－首项）÷项数＋1。从1开始，连续的n个奇数相加，总和＝n×n，如：1＋3＋5＋7＝4×4＝16，……

　　7、几何边端

　　单边线型植树公式(两头植树)：

　　棵树=总长÷间隔+1；

　　总长=（棵树－1）×间隔

　　单边环型植树公式(环型植树)：

　　棵树=总长÷间隔；

　　总长=棵树×间隔

　　单边楼间植树公式(两头不植)：

　　棵树=总长÷间隔-1；

　　总长=（棵树+1）×间隔

　　植树不移动公式：

　　在一条路的一侧等距离栽种m棵树，然后要调整为种n棵树，则不需要移动的树木棵树为：（m－1）与（n－1）的最大公约数＋1棵；

　　方阵问题：

　　最外层总人数＝4×（N－1）

　　相邻两层数量相差8

　　n阶方阵的总人数为n*n

　　8、行程问题

　　火车过桥核心公式：

　　路程＝桥长＋车长（火车过桥过的不是桥，而是桥长＋车长）

　　相遇追及问题公式：

　　相遇距离＝（速度1＋速度2）×相遇时间追及距离＝（速度1－速度2）×追及时间

　　队伍行进问题公式：

　　①队首→队尾：

　　队伍长度=（人速＋队伍速度）×时间；

　　②队尾→队首：

　　队伍长度=（人速－队伍速度）×时间

　　流水行船问题公式：

　　顺速＝船速＋水速，逆速＝船速－水速

　　往返相遇问题公式：

　　①两岸型两次相遇：

　　S＝3S1－S2，（第一次相遇距离A为S1，第二次相遇距离B为S2）

　　②单岸型两次相遇：

　　S＝（3S1＋S2）/2，（第一次相遇距离A为S1，第二次相遇距离A为S2）；

　　③左右点出发：

　　第N次迎面相遇，路程和＝（2N－1）×全程；

　　第N次追上相遇，路程差＝（2N－1）×全程。

　　④同一点出发：

　　第N次迎面相遇，路程和＝2N×全程；

　　第N次追上相遇，路程差＝2N×全程。

　　等距离平均速度：

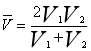
　　9、几何特性

　　三角形三边关系公式：

　　两边之和大于第三边，两边之差小于第三边；

　　直角三角形勾股定理：

　　直角三角形中，两直角边的平方和等于斜边的平方；常用勾股数：（3、4、5）（5、12、13）（6、8、10）

　　内角和定理：

　　正多边形内角和定理，n边形的内角的和等于：（n-2）×180°(n≥3且为整数）；

　　已知正多边形内角度数，则其边数为：360°÷（180°-内角度数）。

　　几何面积和体积：

　　①长方体的表面积=2ab+2ac+2bc

　　②梯形面积

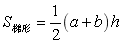
　　③球的表面积

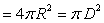
　　④三角形面积

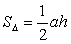
　　⑤平行四边形面积

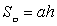
　　⑥圆柱的表面积

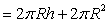
　　⑦球的体积

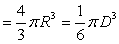
　　⑧圆柱的体积

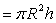
　　⑨椎体的体积

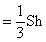
　　若将一个图形尺度扩大为N倍，则：

　　对应角度不变；

　　对应周长变为原来的N倍；

　　面积变为原来的N*N倍；

　　体积变为原来的N*N*N倍。

　　10、经济利润

　　利润＝售价－进价

　　利润率＝利润÷进价

　　总利润＝单利润×销量售价＝进价＋利润＝原价×折扣

　　11、溶液问题

　　溶液＝溶质＋溶剂

　　浓度＝溶质÷溶液

　　溶质＝溶液×浓度混合溶液的浓度＝（溶质1＋溶质2）÷（溶液1＋溶液2）