十字交叉法是数学运算、资料分析偶尔会用到的一种解题思路，运用它可以达到有效提速。“十字交叉法”，即通过十字图对A/B=（r-b）/（a-r）进行简化运算（令a＞b），如图所示：

　　图中的数学思路，不少同学在学生时代都接触过，所以觉得很熟悉。“十字交叉法”实际上就是方程法的简化，将运算思路用一种简单的示意图表示出来，简化分析和计算过程，提高计算速度。

　　数量关系中如何迅速辨别考题是否适用十字交叉，做到快速套用解题？第一，它主要运用于经济利润、溶液问题、比值的混合问题等；第二，考题共同特征是“题干给出了两个量和这两个量的平均值，最后求两个量的比例”。

　　这类问题就可以尝试用“十字交叉法”解题，具体如何运用看几道例题。

　　1.十字交叉法与溶液问题

　　【例题1】某项实验，需要使用不同的A和B两种氯化钠溶液配制成浓度为15%的氯化钠溶液，已知A溶液的浓度是B溶液的5倍，且若将50克A溶液和250克B溶液混合即可完成配置，那么A溶液的浓度是多少？

　　A、45%

　　B、40%

　　C、35%

　　D、30%

　　【特征分析】

　　根据题干可知，题干给出了A和B溶液的混合浓度（即A溶液浓度和B溶液浓度的平均值），且根据题干可知A的浓度和B的浓度，符合用十字交叉法的题干特征。

　　【解题思路】

　　A和B混合后的浓度为15%，混合前A溶液的浓度是B溶液的5倍，则假设B溶液的浓度为x%，则A溶液的浓度为5x%，混合后的浓度15%是总体比值，A和B溶液的浓度是部分比值，则根据十字交叉法可得：

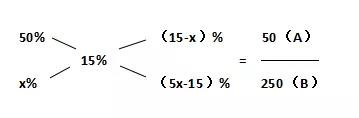
　　解得x=9，则A溶液的浓度为5×9=45，故答案为A。

　　2.十字交叉法与基本比值

　　【例题2】某单位为全体员工进行体检，平均体重是57.5公斤，其中，男员工的平均体重为62.5公斤，女员工的平均体重为55.5公斤。则该单位的男、女员工的人数之比为：

　　A、2:5

　　B、2:7

　　C、7:2

　　D、5:2

　　【特征分析】

　　根据题干可知，题干给出男生平均体重和女生平均体重的两个量，以及男女生的总体平均值，符合十字交叉法的题干特征。

　　【解题思路】

　　用十字交叉法进行解题，可得：

　　因此男、女员工的人数之比为2:5，故答案为A。

　　3.十字交叉法与经济利润

　　【例题3】某商店花10000元进了一批商品，按期望获得相当于进价25%的利润来定价。结果只销售了商品总量的30%。为尽快完成资金周转，商店决定打折销售，这样卖完全部商品后，亏本1000元，问商店是按定价打几折？

　　A、九折

　　B、七五折

　　C、六折

　　D、四八折

　　【特征分析】

　　根据题干可知，卖出的30%按照25%的利润来定价，卖出的70%按照利润率为x%来定价，总亏损1000元可知总的利润率为-10%，则该题符合十字交叉法的题干特征，可用十字交叉法解题。

　　【解题思路】

　　该商品的售价有两种情况，一种是按25%的利润来定价，一种是按打折后的售价，根据亏损了1000元可知利润率为负的即1000/10000=-10%，假设打折后的利润率为x%，按照25%的利润定价的商品买了30%，则按照打折的利润卖了70%，则：

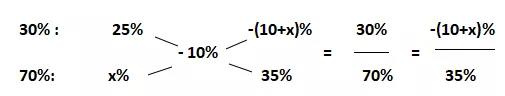
　　解得x=-25，则打折后的利润率为-25%，假设商品的进价为100，则定价为100（1+25%）=125，打折后的售价为75元，则打的折扣为75÷125=0.6即六折。故答案为C。

　　以上，对于十字交叉法，第一次理解也许会有点困难，但实际上它的原理并不复杂，是一种基础方法。它的运用非常灵活，适用于数学运算的多种题型，还有资料分析的“混合增长率”相关考题，也可以结合十字交叉法原理加以理解。

　　方法要能够真正掌握，先要理解其原理，再是多加运用，所以，在复习的过程中要多多了解并尽可能掌握一些技巧，反复运用，考场上才更有可能“赢过时间”，达到事半功倍的效果哦！